Parte integrante do SIG-R, a BDGD (Base de Dados Geográfica da Distribuidora) é um modelo robusto para representar os ativos das distribuidoras de energia elétrica, com diversas de suas estruturas georreferenciadas. No entanto, o grande volume de dados e a complexidade das análises geoespaciais podem representar um desafio, seja ao trabalhar apenas com as informações da BDGD ou ao enriquecê-las com dados geográficos provenientes de outras fontes.
Para enfrentar esses desafios, a Norven, referência em inovação no uso de dados, aplica ferramentas avançadas de computação científica. Entre elas, destaca-se o KDTree, uma estrutura de dados especializada no particionamento espacial em forma de árvore binária de busca. Essa abordagem é particularmente eficiente para cálculos de distância em duas ou três dimensões, reduzindo significativamente os custos computacionais e viabilizando análises complexas de forma otimizada.
O KDTree organiza os dados espaciais em regiões hierárquicas, utilizando hiperplanos para particionar o espaço em duas metades equilibradas em cada nível da árvore. Cada nó da árvore representa uma partição e armazena um ponto do espaço. Durante uma busca, como a identificação do ponto mais próximo de um ponto de consulta, o KDTree elimina rapidamente regiões inteiras que não contêm a solução, reduzindo drasticamente o número de comparações necessárias.
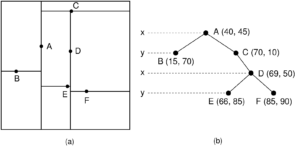
Fonte: https://opendsa-server.cs.vt.edu/ODSA/Books/Everything/html/KDtree.html
Essa eficiência é particularmente evidente em datasets de alta densidade, onde o método ingênuo de busca ponto a ponto seria inviável devido ao alto custo computacional. O custo adicional da construção inicial da árvore é amplamente compensado pela rapidez das buscas subsequentes.
Aplicação do KDTree na BDGD
Para demonstrar a aplicação do KDTree, consideremos o cálculo das distâncias entre Pontos Notáveis (PONNOT) e Segmentos do Sistema de Distribuição de Média Tensão (SSDMT) na cidade de Belo Horizonte. O objetivo é identificar a coordenada do segmento de média tensão mais próximo de cada ponto notável.
Representação de um corte do mapeamento de PONNOT (Vermelho) e SSDMT (Amarelo).
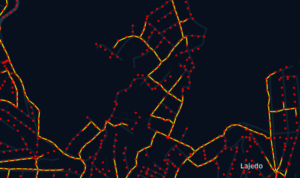
Definindo o número de PONNOTs por P e SSDMT como S, temos um cálculo de distância euclidiana para cada um desses elementos de forma direta:
Operações Diretas =P(x,y) . S(x,y)
Já com a utilização do KDTree, cada “andar” da árvore gerada dividirá a quantidade de P’s de forma exponencial, tendo sua altura máxima, representada por h e, definida por:
N°Andar = P/2h h = log2(P)
Operações KDTree = P(x,y) . log2S(x,y) + S(x,y) . log2S(x,y)
Dessa maneira, é possível perceber que há redução da escala de P(x,y) e S(x,y) para sua busca em árvore binária cruzada entre P para cada S, sendo a busca do primeiro na árvore do segundo somado com a busca do segundo em sua própria árvore, já que o elemento de análise é o P em relação ao S. Em termos computacionais na terminologia do Big-O, podemos considerar as operações diretas como O(P . S) e o KDTree como O(log2S . (P + S)).
Considerando agora o cenário para vincular 200 mil PONNOTs e 135 mil SSDMTs presentes no município de Belo Horizonte. A complexidade do tempo de execução do método direto e com KDTree será:
Odireto = O(200mil . 135mil) = 27 bilhões de operações.
OKDTree = O(log2(135mil) + (200mil + 135mil)) = 5.7 milhões de operações.
O uso do KDTree é cerca de 5000 vezes mais rápido do que a abordagem direta, evidenciando sua eficiência e adequação para processos que demandam alto desempenho. O grande benefício dessa performance é conseguir realizar cálculos massantes de forma extremamente rápida e vincular elementos da BDGD não só pelos campos, mas também pela sua geometria.
Integração do KDTree
Além de acelerar cálculos de distância, o KDTree é amplamente utilizado em diversas aplicações para a BDGD, como em algoritmos de modelagem preditiva, a exemplo do KNN (K-Nearest Neighbors), que utiliza distâncias para classificação e regressão, e em técnicas de clusterização, como KMeans e DBSCAN, que se beneficiam da eficiência do KDTree ao calcular distâncias entre elementos para agrupamento. Essas aplicações destacam a relevância do KDTree como uma ferramenta indispensável na otimização geoespacial, especialmente em contextos de grandes volumes de dados e integração de informações de diferentes fontes.
A Norven reafirma seu compromisso com a inovação ao adotar tecnologias como o KDTree para enfrentar a complexidade da BDGD. Essa abordagem combina eficiência computacional e métodos avançados, possibilitando análises mais rápidas e soluções assertivas, reforçando sua posição como líder em inovação no uso de dados e transformação digital.